Course XLIII - Teaching 16: Tarot Key

You can use the Tarot not only at random, because through certain operations you can use its Figures and Cards to reveal future and secret events.
So, the operator must know three numbers that are fundamental in whatever game or spread.
In diagram you see the order of Figures and Suit Cards, using conventional letters to name and situate them.
First fundamental number, TX: it has to be the result of the power number to use, related to the matter at issue.
Second fundamental number, TX1: refers to the object at issue, reduced to express a number and in relation to the aim of your quest.
Third fundamental number, TX2: determined by a number, or combination of similar numbers, or characteristic numbers of the operator.
These three numbers correspond to respective Figures placed and ordered as in Diagram: TX is ever on the right; TX1, upside-down; and TX2, upright.
If you determine the number of whatever Figures and the result is 22 or less, place the Figure corresponding to the number that you got; if the number is higher than 22, add the absolute values of their numbers, and place the Figure corresponding to this addition.
Hypothesis: if the number that you got is 27, add 2 and 7 = 9. So, 9 will be the Figure to place. Take notice: likewise it occurs with Suit cards. If you determine the number and the result is 14, place the corresponding card. If the number is higher, repeat the operation as above.
Hypothesis: if the number is 19, add 1 and 9 = 10. So, 10 will be the card to place.
After you determine the three Figures, that is, TX1, TX and TX2, you must find three basic numbers, that is, X, X1 and X2, which are not located in the Diagram because they do not correspond to any Figure or card. So, you get:
X1 = TX x TX1 x TX2.
You should reduce this product, by adding absolute values of its numbers, as in the following hypothesis:
If TX1 x TX x TX2 = 365,
you should add 3 and 6 and 5 = 14.
In which case X1 = 14.
Analogically, to determine the value of X:
X = TX x TX. Hypothetically, if TX = 9,
so, 9 x 9 = 81.
Also you should reduce by adding its absolute numbers:
8 and 1 = 9;
so, X = 9.
Finally, X2 = TX1 x TX2. You should reduce this product as above:
If TX1 x TX2 = 132,
then 1 and 3 and 2 = 6.
So, X2 = 6.
In short:
X1 = TX1 x TX x TX2;
X = TX x TX;
X2 = TX1 x TX2,
by reducing products as explained above.
As much TX1 as TX and TX2 must be different. For instance, if TX2 is equal in value to TX, then you should add one unit. If TX is 8, and TX2 is also 8, you should add one to this number, in which case TX2 = 9. If X is 5, and X2 is also 5, you should add one unit, that is, 5 and 1 = 6.
Once you get the three Figures and three basic numbers, proceed to place twelve Suit cards as in Diagram, according to the following rules:
First determine the fundamental Suit, which will be that belonging to card A.
So, keep in mind the following diagram:

To determine the Suit corresponding to A, add basic numbers X1, X and X2 and later add absolute numbers of the said addition.
If the result of the last addition is 4, or less, it will correspond to the Suit according to the graphic. So, if the addition is hypothetically:
X1 and X and X2 = 10,
1 and 0 = 1.
So, Hearts will be Suit of A.
If the result of the addition is higher than 4, you will divide the product by two; If the quotient even is higher than 4, you will divide it again by two, up to this result: 4, or less. If the result of this division (or of these divisions) is a quotient with decimals, then the Suit number will be by approximation.
Hypothetically, if X1 and X and X2 = 25, we will have 2 and 5 = 7. 7 divided by 2 = 3,50; 3 will be the number to determine the Suit, in this case, Spades.
In short, Suit of A is equal to X1 + X + X2, by reducing absolute values of the product of additions in the above-mentioned way.
To determine the number of A, add TX1 and TX and TX2, by reducing values of the product of the addition to a number that will not be higher than 14.
The Suit of B will be equal to that of A, except that its number is equal to that of A, in which case it will have the following Suit, in the above-established order of the graphic. For instance, if the Suit of A is Hearts, and its number is equal to that of A. then it will be Clubs; if A is Diamonds, in the same case would be Hearts.
To determine the number of B: B = A + TX1 + TX + TX2.
The Suit of C will be equal to that of B, except that it has the same number; in which case, and always in accordance with the order of the graphic, it would be the following.
Likewise this rule is applicable to all subsequent cards.
Number of C is equal to A + B.
Number D is equal to B + C.
Number of E is equal to B + C + D.
Number of F is equal to A + B + C + D + E.
Number of G is equal to TX1 + TX + TX2; as above, add absolute values of products of the addition, with the usual reduction; you determine the Suit as above. If cards of the number are already places in those four Suits, then put the number immediately higher than the corresponding Suit.
You get the card number:

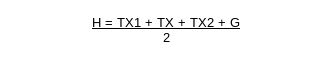
If the quotient is higher than 2, then divide it successively by this number until you get a quotient lower that 2 and higher than the unit. If the result is 1,75, then you will place the number 2; if the quotient is lower than 1,75, then you will put the Ace.

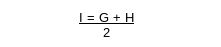
Likewise, to determine H. If the quotient is 1,75, then place 2; if it is lower, than an Ace.

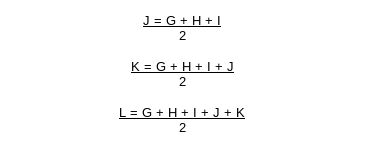
In these cases proceed as above to determine the number of G until getting a number higher that 1 and lower than 2, by dividing by 2.
The card A, even or odd, should be upright. If A is even, all cards of even number will be upright, and all cards of odd numbers will be upside-down. On the contrary, if A is odd, all odd cards will be upright and all even cards will be upside-down.
To get the number of Resume card, that is, R, add the twelve cards A-L. If the product of this addition is higher than 14, then divide by 2, successively, until getting the quotient of 14, or less; if the result is a decimal fraction, then it will correspond by approximation. If this resulting card is already placed, then put the immediate higher. The Suit will be the result of applying the above-explained rules.
You get S1, S2, S3 and S4 by adding respectively: A, C, E; B, D, F; G, I, K; and H, J.L. If the result of every one of these additions is more than 14, then you will reduce according to above-mentioned rules. The same occurs to determine its suit.